Gradient Boosting (그래디언트 부스팅) for Regression (회귀)

n 개의 Data sample이 있을 때,
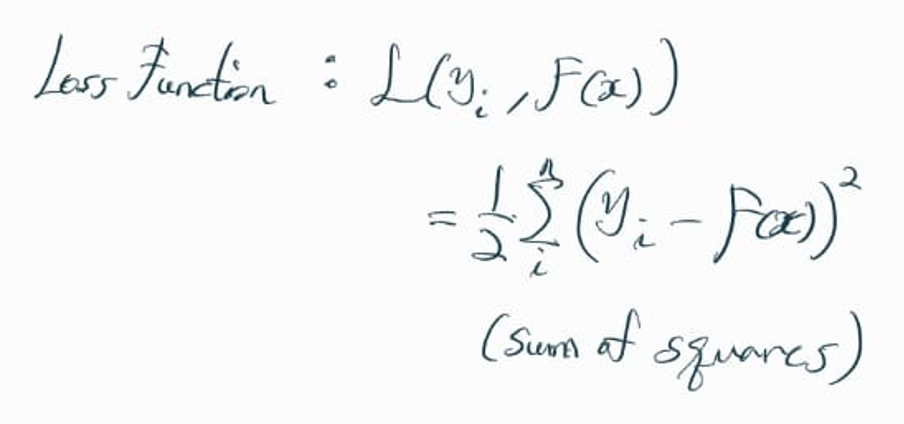
Loss Function (손실 함수) 을 sum of squares에 1/2을 곱한 값으로 정의한다.
1/2를 곱한 이유는, 이후 Gradient Descent 과정에서 2차항의 2가 1/2과 곱해져서 상쇄되기 때문이다.
< Step 1 >

가장 먼저 초기 F0(x)를 구한다.
Gradient Descent로 Loss Function 값을 최소화하는 F0(x)를 구해보면,
그 값은 모든 data sample의 y 값의 평균이 된다.
즉, 이 상태에서 모델은 모든 데이터에 대해
y의 평균으로 예측 (predict) 한다.
< Step 2>

Step 2는 1번 tree 부터, 마지막 M번 tree까지
총 M번 반복된다.
< Step 2 - (a) >

현재 m 번째 tree에서
실제값 yi와, 이전 단계에서의 예측값 F(m-1)(x) 의 차이 (pseudo residual)를 구한다.
< Step 2 - (b) >
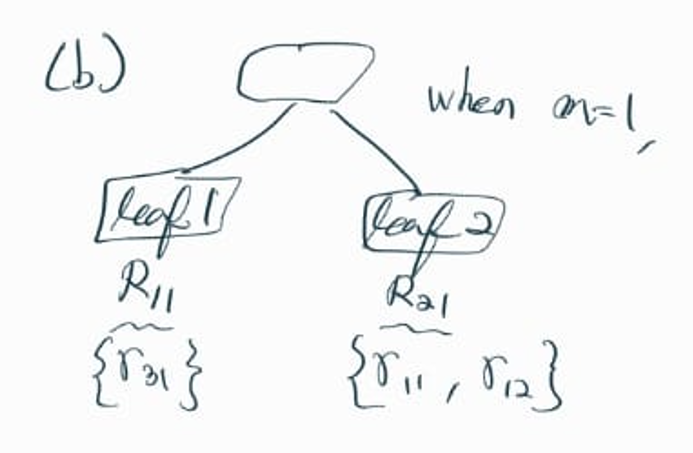
Step2 - (a) 단계에서 구한 residual (잔차) r 값을,
해당 data sample이 속한 leaf node에 할당한다.
< Step 2 - (c) >

m 번째 tree의 j 번째 leaf node 에서,
해당 leaf node에 속한 data sample들의 residuals (잔차) 의 평균을 구한다.
여기서도 "Gradient Descent"를 활용한다.
< Step 2 - (d) >

Step 2 - (c)에서 구한 leaf node의 residuals 평균값에 learning rate를 곱해서,
이전 단계 (m-1)에서 구한 F(m-1)(x)에 더해준다.
그리고 그 값이 F(m)(x)가 된다.
Step 2 과정을 M 개의 tree에 대해서 M 번 반복한다.
< Step 3 >

Step 2를 M번째 tree까지 모두 반복하고 나면, F(M)(x)를 얻게 되는데
이 값이 x에 대한 모델의 최종 y (predict) 값이다.
Gradient Boosting의 작동 방식에 대해 공부하고 나니,
이름에 왜 "Gradient"가 들어가는지 확실히 이해할 수 있었다.
◎ References
< StatQuest, Gradient Boost Part 2 (of 4): Regression Details >
< Paper, Greedy Function Approximation: A Gradient Boosting Machine >
'Data Science' 카테고리의 다른 글
| Linear Regression (0) | 2023.05.01 |
|---|---|
| p-value & p-hacking (0) | 2023.04.28 |
| Conditional Entropy (0) | 2023.04.27 |
| Entropy & Surprise (0) | 2023.04.26 |
| Adaboost (0) | 2023.04.25 |



