Softmax

다중 분류 (Multi-class Classification) 에 사용되는 소프트맥스 (Softmax) 함수에 대해 살펴보았다.

 

Softmax 함수는 시그모이드 (Sigmoid) 의 일반화 된 버전이라고 생각할 수 있다.

 

Sigmoid가 이진 분류 (Binary Classification) 에 주로 활용된다면,

Softmax는 다중 분류에 주로 활용된다.

 

신경망 (Neural Network) 의 출력값을, 확률 (Likelihood) 로 변환시켜주는 역할을 한다.

 

 

 

---

 

 

K 개의 클래스가 존재하는 데이터에서, Softmax의 유도 과정을 살펴보면 아래와 같다.

 

 

먼저 i-클래스의 확률 p(i)와 k-클래스의 확률 p(K)의 비율을 e^t(i)로 정의한다.

 

t(i) = log( class-i의 확률 p(i)와 class-K의 확률 p(K)의 비율 )

 

 

 

K를 제외하고, m = 1부터 K-1까지 e^t(m)의 합을 구한다.

 

m = 1 부터 K-1 까지, e^t(m)의 합

 

 

 

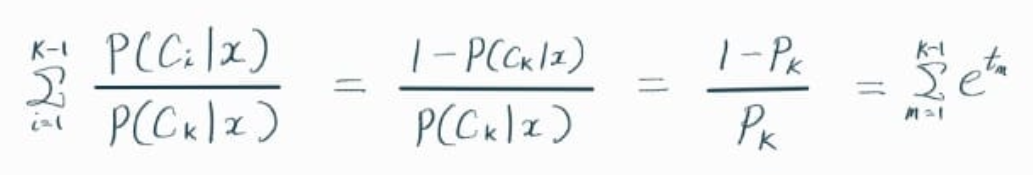
위 식을 변형해서, p(K)를 계산한다.

 

p(K)

 

---

 

 

 

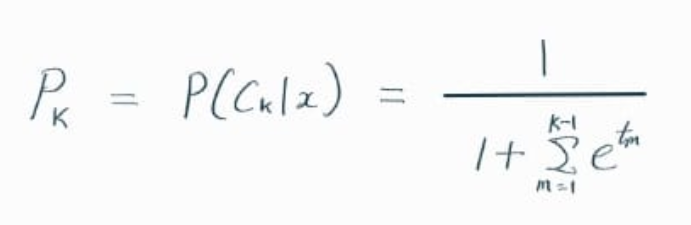
제일 처음에서 정의했던 위의 식을 활용해서,

아래와 같이 p(i)를 정리하면

결국 p(i) = Softmax( t(i) ) 의 형태로 나타나는 걸 알 수 있다.

 

P(i) = Softmax( t(i) )

 

 

---

 

Neural Network에서, 입력값 x에 대해 각 클래스 별로 출력값 t가 나온다.

i번 클래스라고 하면, t(i)가 나온다.

이 값을 softmax에 넣으면, 확률 p(i)가 나오게 된다.

 

이 때, 아래 그림과 같이 p(i)를 t(i)로 미분해보자.

 

p(i)를 softmax에 들어가기 전 출력값 t(i)로 미분

 

위의 미분에 활용된 공식

 

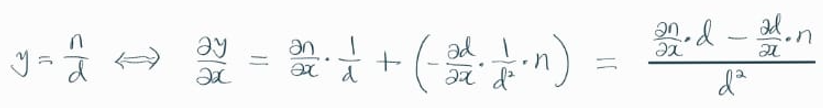
신기하게도 p(i) * ( 1 - p(i) ) 라는 결과가 나온다.

 

---

 

◎ References

 

< Logistic Regression >

 

< 한 페이지 머신러닝, logit, sigmoid, softmax의 관계 >

 

< StatQuest, The SoftMax Derivative, Step-by-Step!!! >