역전파(Backpropagation) 알고리즘의 구체적인 진행 과정이
갑자기 너무 헷갈려서,
다시 공부한 내용을 정리해보았다.
이 자료를 보면서, 역전파에 대해 더욱 깊게 이해할 수 있었다.
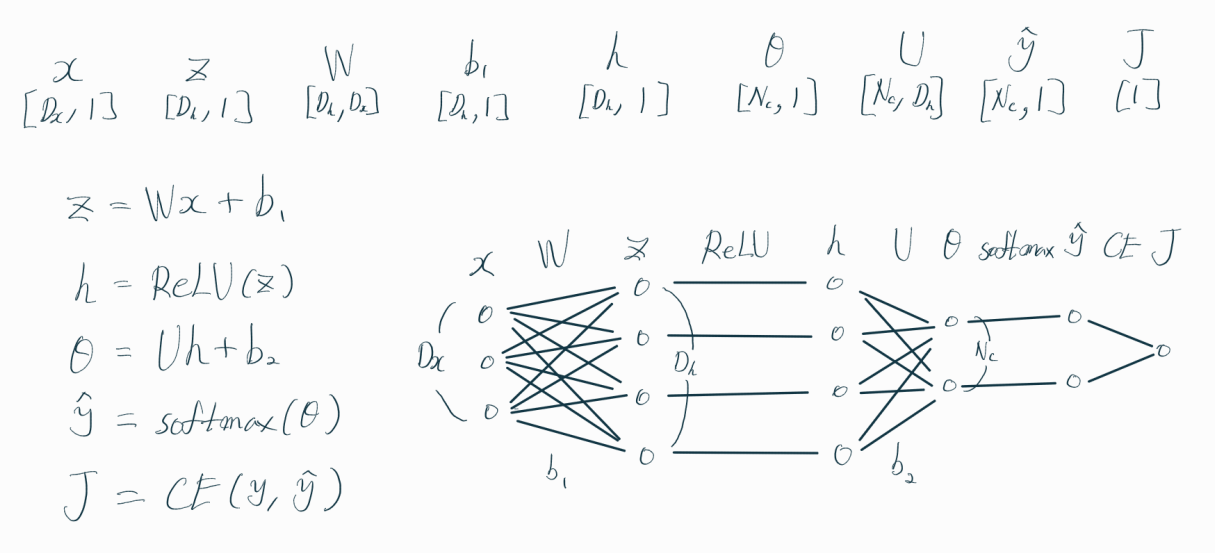
위 그림처럼 생긴 신경망(Neural Network)이 있다고 해보자.
다중분류(Multiclass Classification) 문제라고 가정하고,
은닉층(hidden layer) 활성화함수(activation function)으로 ReLU를,
출력층(output layer)의 활성화함수는 softmax를 사용한다.
손실함수(Loss Function)로는 CE(Cross Entropy)를 활용한다.
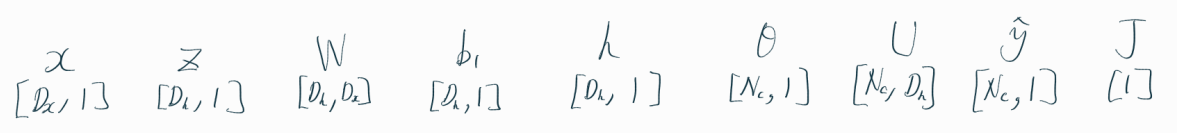
위 그림은 각 변수들의 차원(dimensions)을 나타낸다.
W는 입력층과 은닉층 간 가중치들을 나타내고,
U는 활성화 함수(activation function)를 거친 은닉층과
활성화 함수를 거치지 않은 출력층(Output Layer) 간의 가중치를 나타낸다.
신경망 세팅을 마쳤다.
역전파를 알아보기 전에, 먼저 여러 형태의 미분에 대해 살펴봤다.
역전파를 제대로 이해하기 위해서는,
미분의 연쇄법칙(Chain rule) 및
스칼라(scalar), 벡터(vector), 행렬(matrix) 간의 미분에 대해 알고있어야 한다.
아래의 수식들은 역전파 알고리즘의 이해를 위해 필요한,
연쇄법칙 및 미분에 관한 수식들이다.

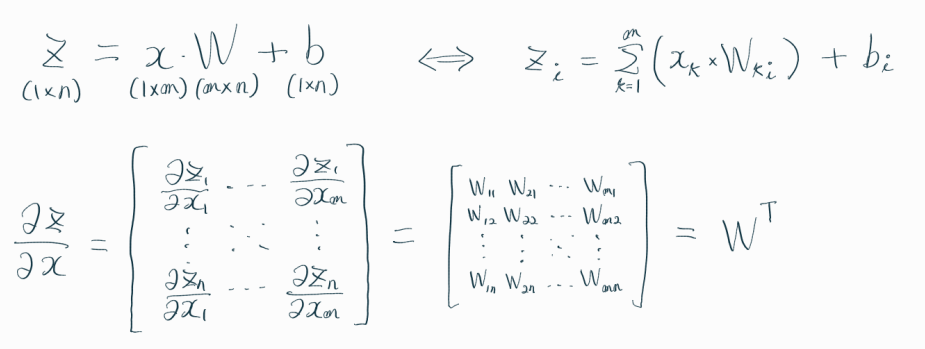

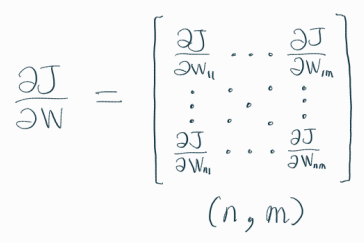
역전파를 통해 하고자 하는 것은 결국 가중치(weight) 업데이트이다.
즉, 손실함수 J를 가중치 W로 미분한 결과를 구하는 것이 주요 목적이다.
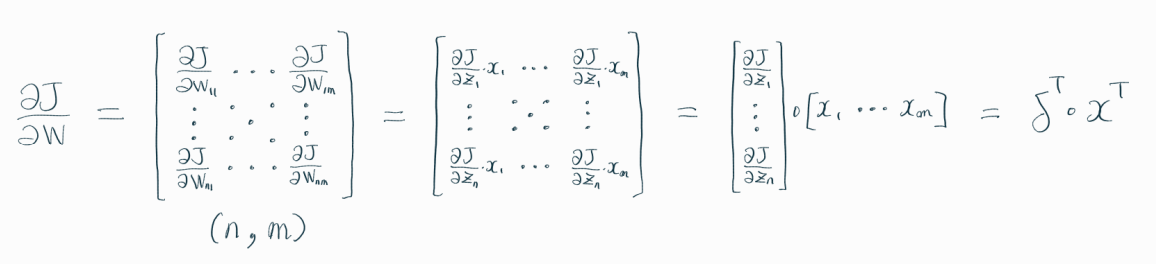
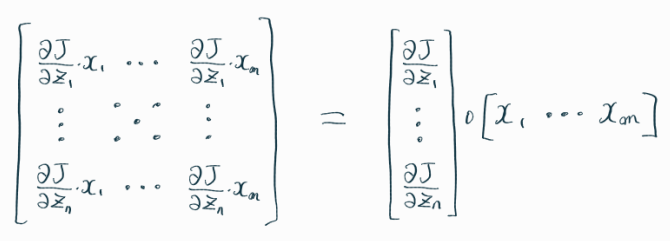
위의 수식을 이해하는 것이 가장 까다로웠는데,
살펴보면 아래와 같다.
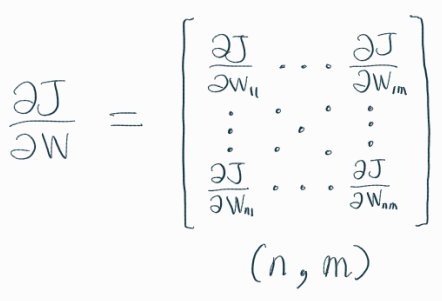




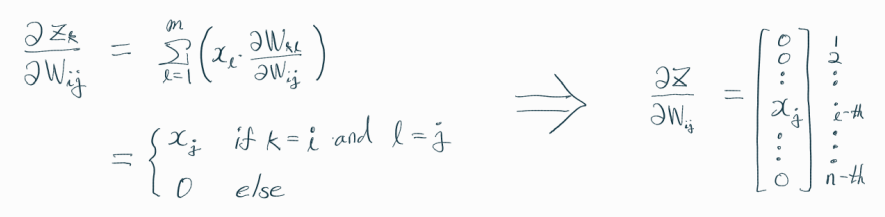
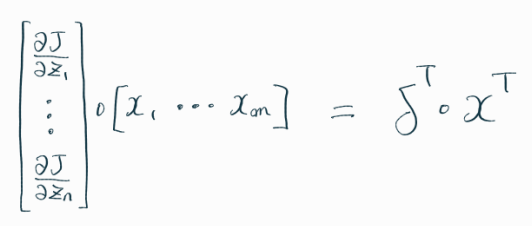
이제 역전파(Backpropagation) 알고리즘을 살펴보자.
"역전파"라는 이름답게
마지막 단계인 Loss Function부터 입력층까지, 역방향으로 진행된다.
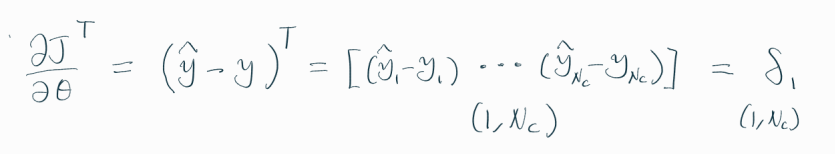
손실 함수(CE)를 theta에 대해 미분하면, 신기하게도 (predicted - observed) 값인 음의 잔차(-residual) 형태가 나온다.
위의 계산을, 손실 함수를 가중치 U로 미분하는 데에 활용해보자.
손실 함수(CE)를 U에 해당하는 가중치로 편미분하면, 위와 같이 표현할 수 있다.
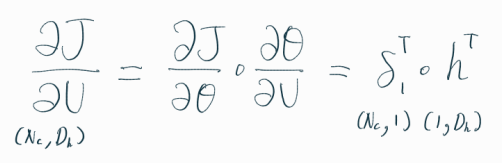
위의 수식이 이해가 가지 않는다면, 그보다 앞서 정리한 수식들을 다시 살펴보고 오면 좋다.
다음으로 손실함수 J를 가중치 행렬 W에 대해 미분해보자.
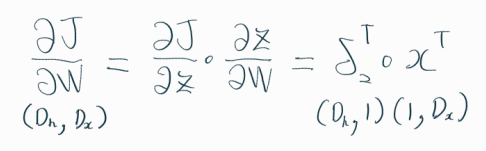
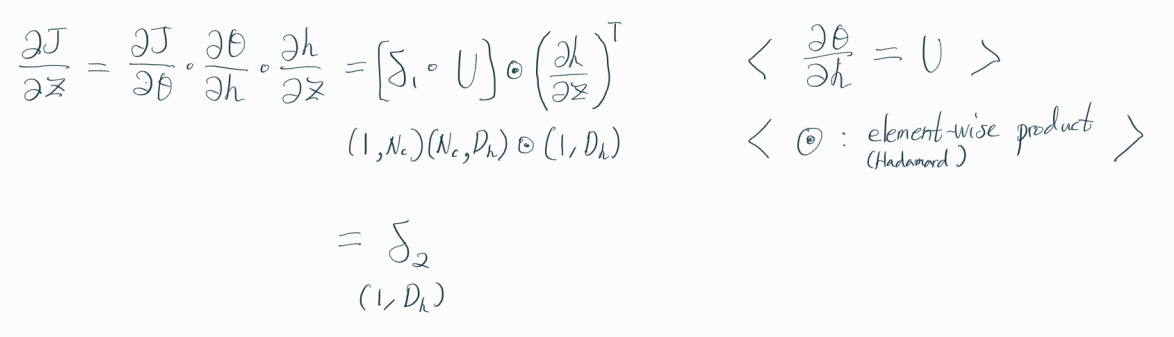
계산 과정에서 볼 수 있듯,
역전파 알고리즘은 앞에서 계산한 값들을
뒤에서 계속 활용하기 때문에 효율적이다.
위에서 구한 dJ/dW와 dJ/dU를 활용해서,
아래와 같이 가중치 행렬 W와 U를 업데이트 할 수 있다.

위 수식에서 B는 batch size를 의미한다.
여기서 하나의 배치(batch)에 포함되는 모든 데이터에 대해 계산하고,
모두 더해주는 과정이 포함되어 있따.
※ 그래서 Batch size가 커질수록, 연산에 더욱 큰 메모리를 요구한다.
그래서 너무 큰 batch size는 메모리 에러(MemoryError: Unable to allocate ~~)를 발생시킬 수 있다.
이렇게 Backpropagation이 진행되는 과정을 자세하게 복습해봤다.
그 과정에서 헷갈렸던 부분을 잘 정리할 수 있었다.
◎ References
< Kevin Clark, Computing Neural Network Gradients >
< 아이언웨일의 웨어하우스, [딥러닝] 역전파를 공부시 필요한 자료 >
'Data Science' 카테고리의 다른 글
| Permutation Importance (0) | 2023.06.03 |
|---|---|
| Logistic Regression (0) | 2023.05.31 |
| Pearson's Correlation (0) | 2023.05.19 |
| Covariance (0) | 2023.05.18 |
| SVM (Support Vector Machine) (0) | 2023.05.17 |


