SVM (Support Vector Machine)

margin과 optimal hyperplane 등에 관한 개념 및 수식은

이 블로그 글을 보고 많이 이해할 수 있었다.

 

아래에서는 kernel에 관해 학습한 내용 위주로 정리해보았다.

 

 

Polynomial kernel

 

x가 input dataset인 X의 data이고, n개의 feature를 갖고있을 때

 

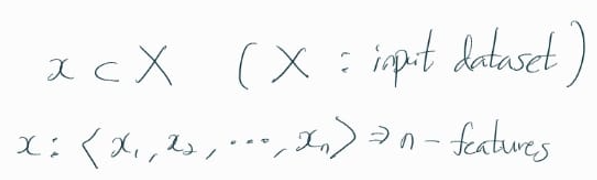
Polynomial kernel 은 다음과 같이 정의된다.

Polynomial kernel

 

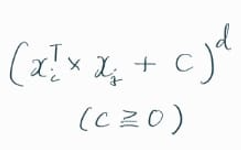
c는 0 이상의 임의의 상수를 설정할 수 있고,

d는 차원 (dimension) 을 의미하는 변수이다.

 

 

두 input vectors 간 inner product를 고려하면,

n-features

이런 형태가 된다.

 

 

좀 더 쉽게 이해하기 위해,

d = 2 (2차원), n = 1 (1개의 feature로만 이뤄진 입력 데이터) 로 설정하면

 

 

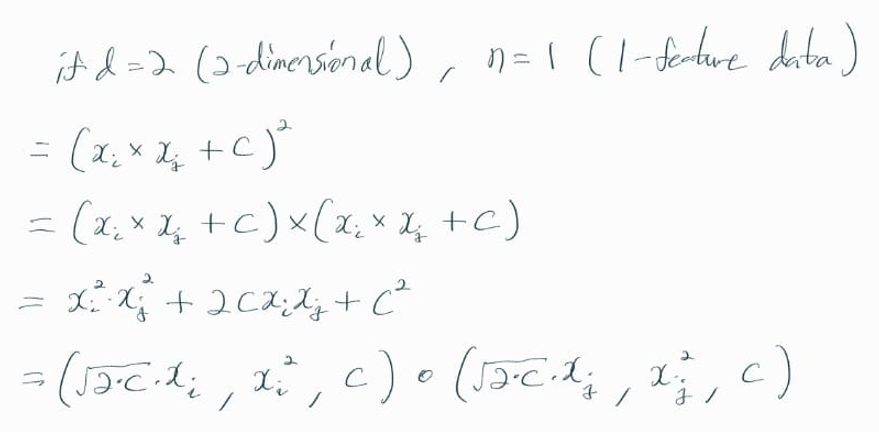
이렇게 두 벡터 간 내적으로 나타낼 수 있다.

 

axis 1 & 2

 

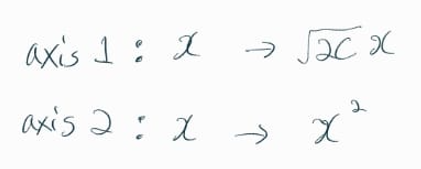
즉, 1차원의 어떤 값 x를

축 1 (axis1) 에서는 x에 root(2c) 만큼 곱하고,

축 2 (axis2) 에서는 x에 제곱을 한다고 해석할 수 있다.

 

그렇게 확장된 2차원 공간에서 SVM을 통해 데이터를 분류할 수 있다.

 

특정 조건이 아닌, 일반화된 수식은 여기서 확인할 수 있다

 

 

 

 

RBF (Radial basis function) kernel

 

RBF kernel은 위의 Polynomial kernel을 무한대의 차원으로 확장한다.

 

RBF kernel의 정의는 아래와 같다.

RBF kernel

 

수식을 간단하게 만들기 위해, x가 1차원이라고 가정하면,

 

 

위와 같이 두 벡터 간의 내적으로 표현할 수 있다.

 

중간에 e^(ab)를 테일러 급수 전개 (Taylor Series expansion)를 통해 변환하는 과정이 있다.

테일러 급수 전개 (Taylor Series expansion)

 

 

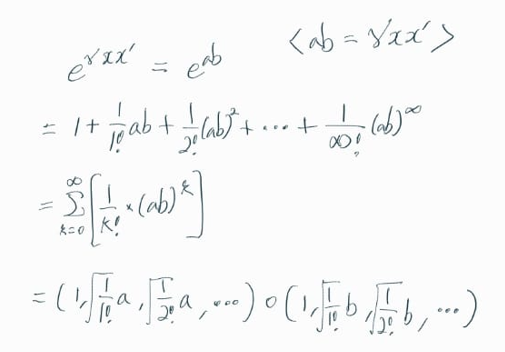
아래의 RBF kernel 수식을 살펴보면,

RBF kernel (n-feature=1)

 

Polymial kernel 수식의 차원이 무한대(infinity)로 확장된 것과 동일한 형태라는 것을 알 수 있다.

Polynomial kernel (n-feature=1, d=2)

 

 

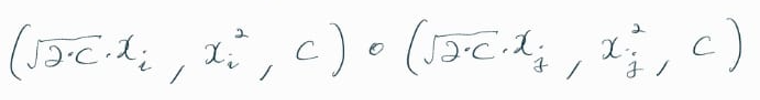
특정 조건이 아닌, 일반화된 수식은 여기서 확인할 수 있다

 

 

---

 

 

SVM에서는 이런 kernel들을 적용해서,
non-linear 한 형태의 data들의 차원(dimension)을 확장시켜
모델 성능을 높인다고 할 수 있다.

 

 

---

 

◎ References

 

< StatQuest, Support Vector Machines >

 

< Wikipedia, Polynomial kernel >

 

< Wikipedia, Radial basis function kernel >

 

< ratsgo's blog, 서포트 벡터 머신 (Support Vector Machine) >