피어슨 상관계수 (Pearson's Correlation)
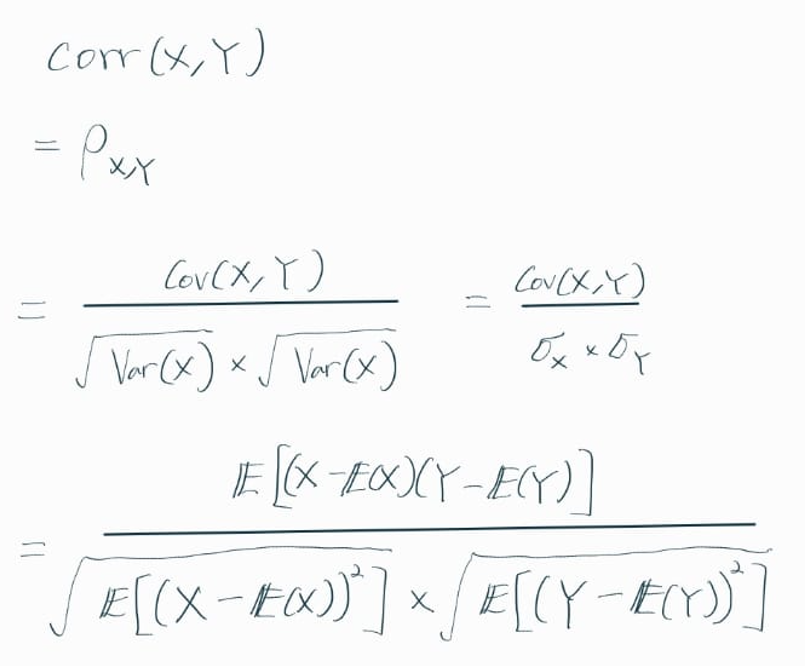

표본(Sample)에서의 상관계수 수식에서 등장하는
standard scores란,
x가 X의 평균(mean)에서 얼마만큼 떨어져있는지를
Sx (표준편차, standard deviation) 의 척도로 나타낸 값이다.
먼저 상관계수 corr(X, Y)의
양수(positive)와 음수(negative)의 의미를 살펴보면,
1. corr(X, Y) > 0
피어슨 상관계수 값이 0보다 크다면,
이는 어떤 data point의 X 값이 X의 평균보다 크다면,
Y 값 또한 Y의 평균보다 큰 경향을 나타낸다는 뜻이다.
2. corr(X, Y) < 0
피어슨 상관계수 값이 0보다 작다면,
이는 어떤 data point의 X 값이 X의 평균보다 크다면,
Y 값은 Y의 평균보다 작은 경향을 나타낸다는 뜻이다.
공분산(Covariance)은 data의 scale에 따라 값이 변하지만,
피어슨 상관계수(Pearson's Correlation)는
data의 scale이 변해도 그 값이 일정하게 유지된다.
예를 들어, X data의 scale을 2배로 늘리면
분자(numerator)의 cov(X, Y) 값이 2배로 늘어나지만,
분모(denominator)의 std(X)값 또한 똑같이 2배로 늘어나기 때문에
scale에 관계없이 값이 일정하게 유지된다.
위의 수식을 통해 구한 상관계수 값(correlation coefficient)의 크기는,
그 값의 크기(절댓값)가 클수록
상관관계가 더 높다는 것을 의미한다.
하지만 두 변수 X, Y 간의 상관계수 값이
정말 두 변수 간애 유의미한 상관관계를 나타낸다고 판단하려면,
통계적 검증이 필요하다.
그 검증 방식에는
▷ t-분포 (student's t-distribution),
▷ 최소자승 회귀분석 (least squares regression analysis) 등
다양한 검증 방식이 있다.
검증 방식들에 대한 자세한 내용은 여기서 확인할 수 있다.
◎ References
< Wikipedia | Pearson correlation coefficient >
< StatQuest | Pearson's Correlation, Clearly Explained!!! >
'Data Science' 카테고리의 다른 글
| Logistic Regression (0) | 2023.05.31 |
|---|---|
| Backpropagation (0) | 2023.05.23 |
| Covariance (0) | 2023.05.18 |
| SVM (Support Vector Machine) (0) | 2023.05.17 |
| CatBoost (0) | 2023.05.13 |



